损失函数

Posted on 2020-07-19 In 机器学习 Views:

1. 概念区分

Loss Function
损失函数 Loss Function

损失函数 Loss Function还分为经验风险损失函数和结构风险损失函数。经验风险损失函数指预测结果和实际结果的差别，通常是针对单个训练样本而言，给定一个模型输出 y^ 和一个真实 y ，损失函数输出一个实值损失y - y^ 。用来评价模型的预测值和真实值不一样的程度，损失函数越好，通常模型的性能越好。不同的模型用的损失函数一般也不一样。结构风险损失函数是指经验风险损失函数加上正则项。

Cost Function

代价函数 Cost Function 通常是针对整个训练集（或者在使用 mini-batch gradient descent 时一个 mini-batch）的总损失。

Objective Function

目标函数 Objective Function 是一个更通用的术语，表示任意希望被优化的函数，用于机器学习领域和非机器学习领域（比如运筹优化）

即：损失函数和代价函数只是在针对样本集上有区别。

2.回归常用损失函数

2.1 均方差损失（MSE）

均方差 Mean Squared Error (MSE)损失是机器学习、深度学习回归任务中最常用的一种损失函数，也称为 L2 Loss。其基本形式如下

$J_{MSE} = \frac{1}{N}\sum_{i=1}^{N}(y_i - \hat{y_i})^2 \\$
原理推导

实际上在一定的假设下，我们可以使用最大化似然得到均方差损失的形式。假设模型预测与真实值之间的误差服从标准高斯分布（正态分布）（ $\mu=0, \sigma=1$ ），则给定一个 $x_i$ 模型输出真实值 $y_i$ 的概率为

$p(y_i|x_i) = \frac{1}{\sqrt{2\pi}}\mathbb{exp}\left (-\frac{(y_i-\hat{y_i})^2}{2}\right ) \\$

进一步我们假设数据集中 N 个样本点之间相互独立，则给定所有 $x$ 输出所有真实值 $y$ 的概率，即似然函数，为所有 $p(y_i \vert x_i)$ 的累乘

$L(x, y) = \prod_{i=1}^{N}\frac{1}{\sqrt{2\pi}}\mathbb{exp}\left (-\frac{(y_i-\hat{y_i})^2}{2}\right) \\$

通常为了计算方便，我们通常最大化对数似然（通过去log,将乘机转为和的形式,方便计算）

$LL(x, y)=\mathbb{log}(L(x, y))=-\frac{N}{2}\mathbb{log}2\pi - \frac{1}{2} \sum_{i=1}^{N} (y_i-\hat{y_i})^2 \\$

去掉与 $\hat{y_i}$ 无关的第一项，将最大化对数似然转化为最小化负对数似然，就可以使用梯度下降等方法对其求最小值了。

$NLL(x, y) = \frac{1}{2}\sum_{i=1}^{N}(y_i - \hat{y_i})^2 \\$

可以看到这个实际上就是均方差损失的形式。也就是说在模型输出与真实值的误差服从高斯分布的假设下，最小化均方差损失函数与极大似然估计本质上是一致的，因此在这个假设能被满足的场景中（比如回归），均方差损失是一个很好的损失函数选择；当这个假设没能被满足的场景中（比如分类），均方差损失不是一个好的选择。

2.2 平均绝对损失 (MAE)

平均绝对误差 Mean Absolute Error (MAE)是另一类常用的损失函数，也称为 L1 Loss。其基本形式如下

$J_{MAE}=\frac{1}{N}\sum_{i=1}^{N}\left | y_i - \hat{y_i} \right | \\$

MAE 损失的最小值为 0（当预测等于真实值时），最大值为无穷大。随着预测与真实值绝对误差 $\lvert y- \hat{y}\rvert$ 的增加，MAE 损失呈线性增长.

原理推导

同样的我们可以在一定的假设下通过最大化似然得到 MAE 损失的形式，假设模型预测与真实值之间的误差服从拉普拉斯分布 Laplace distribution（ $\mu=0, b=1$ ），则给定一个 $x_i$ 模型输出真实值 $y_i$ 的概率为

$p(y_i|x_i) = \frac{1}{2}\mathbb{exp}(-\left |y_i-\hat{y_i}\right|) \\$

与上面推导 MSE 时类似，我们可以得到的负对数似然实际上就是 MAE 损失的形式

$L(x, y) = \prod_{i=1}^{N}\frac{1}{2}\mathbb{exp}(-|y_i-\hat{y_i}|)\\ LL(x, y) = -\frac{N}{2} - \sum_{i=1}^{N} |y_i-\hat{y_i}| \\ NLL(x, y) = \sum_{i=1}^{N} |y_i-\hat{y_i}| \\$

MAE与MSE的比较

1. MSE 通常比 MAE 可以更快地收敛。当使用梯度下降算法时，MSE 损失的梯度为 $-\hat{y_i}$ ，而 MAE 损失的梯度为 $\pm1$ ，即 MSE 的梯度的 scale 会随误差大小变化，而 MAE 的梯度的 scale 则一直保持为 1，即便在绝对误差 $\lvert y_i-\hat{y_i} \rvert$ 很小的时候 MAE 的梯度 scale 也同样为 1，这实际上是非常不利于模型的训练的。当然你可以通过在训练过程中动态调整学习率缓解这个问题，但是总的来说，损失函数梯度之间的差异导致了 MSE 在大部分时候比 MAE 收敛地更快。这个也是 MSE 更为流行的原因。

2. MAE 对于 outlier 更加 robust。我们可以从两个角度来理解这一点：

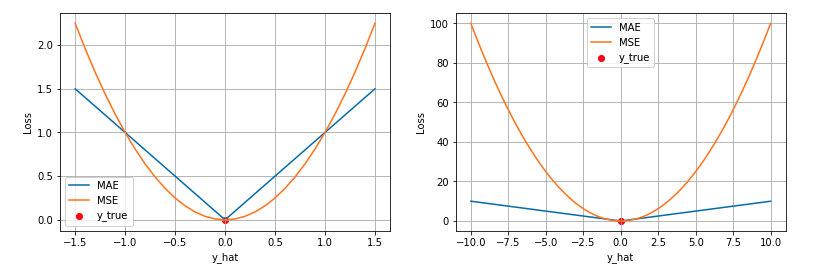
第一个角度是直观地理解，下图是 MAE 和 MSE 损失画到同一张图里面，由于MAE 损失与绝对误差之间是线性关系，MSE 损失与误差是平方关系，当误差非常大的时候，MSE 损失会远远大于 MAE 损失。因此当数据中出现一个误差非常大的 outlier 时，MSE 会产生一个非常大的损失，对模型的训练会产生较大的影响。

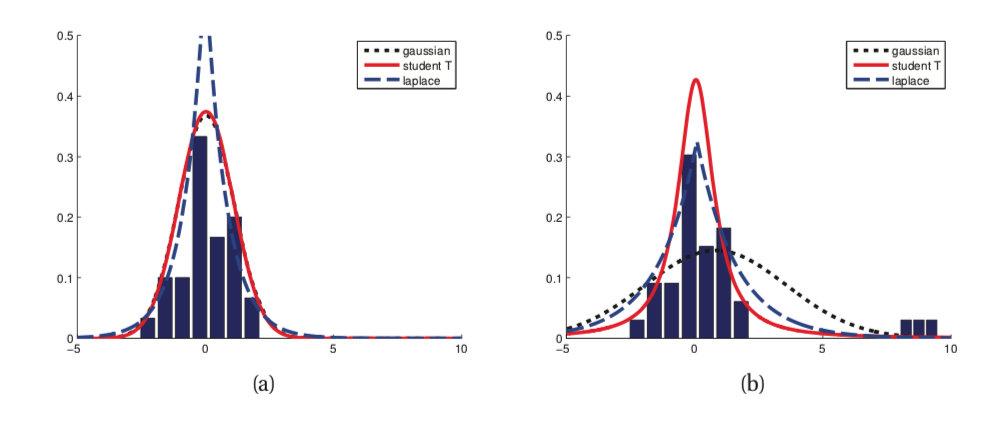
第二个角度是从两个损失函数的假设出发，MSE 假设了误差服从高斯分布，MAE 假设了误差服从拉普拉斯分布。拉普拉斯分布本身对于 outlier 更加 robust，当右图右侧出现了 outliers 时，拉普拉斯分布相比高斯分布受到的影响要小很多。因此以拉普拉斯分布为假设的 MAE 对 outlier 比高斯分布为假设的 MSE 更加 robust。

2.3 Huber Loss

上文我们分别介绍了 MSE 和 MAE 损失以及各自的优缺点，MSE 损失收敛快但容易受 outlier 影响，MAE 对 outlier 更加健壮但是收敛慢，Huber Loss则是一种将 MSE 与 MAE 结合起来，取两者优点的损失函数，也被称作 Smooth Mean Absolute Error Loss 。其原理很简单，就是在误差接近 0 时使用 MSE，误差较大时使用 MAE，公式为

$[å¬å¼]$

上式中 $\delta$ 是 Huber Loss 的一个超参数， $\delta$ 的值是 MSE 和 MAE 两个损失连接的位置。上式等号右边第一项是 MSE 的部分，第二项是 MAE 部分，在 MAE 的部分公式为 $\delta \lvert y_i - \hat{y_i}\rvert - \frac{1}{2}\delta^2$ 是为了保证误差 $\lvert y - \hat{y}\rvert=\pm \delta$ 时 MAE 和 MSE 的取值一致，进而保证 Huber Loss 损失连续可导。

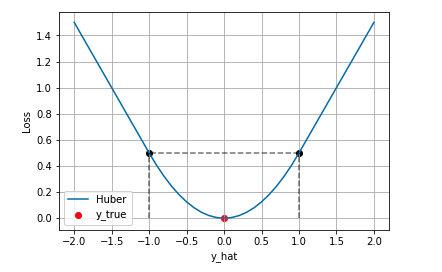
下图是 $\delta=1.0$ 时的 Huber Loss，可以看到在 $[-\delta, \delta]$ 的区间内实际上就是 MSE 损失，在 $(-\infty, \delta)$ 和 $(\delta, \infty)$ 区间内为 MAE损失。

Huber Loss 的特点

Huber Loss 结合了 MSE 和 MAE 损失，在误差接近 0 时使用 MSE，使损失函数可导并且梯度更加稳定；在误差较大时使用 MAE 可以降低 outlier 的影响，使训练对 outlier 更加健壮。缺点是需要额外地设置一个 $\delta$ 超参数。

Huber Loss python实现

# huber 损失
def huber(true, pred, delta):
    loss = np.where(np.abs(true-pred) < delta , 0.5*((true-pred)**2), delta*np.abs(true - pred) - 0.5*(delta**2))
    return np.sum(loss)

3.分类常用损失函数

3.1 交叉熵损失

3.1.1 二分类

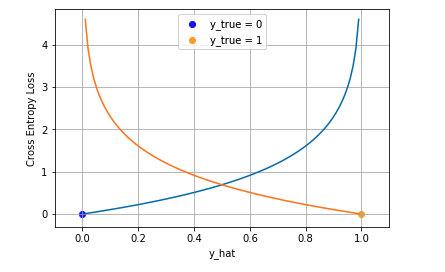
考虑二分类，在二分类中我们通常使用Sigmoid函数将模型的输出压缩到 (0, 1) 区间内 $\hat{y_i} \in (0, 1)$ ，用来代表给定输入 $x_i$ ，模型判断为正类的概率。下图是对二分类的交叉熵损失函数的可视化，蓝线是目标值为 0 时输出不同输出的损失，黄线是目标值为 1 时的损失。可以看到约接近目标值损失越小，随着误差变差，损失呈指数增长。

$NLL(x, y)=J_{CE}=-\sum_{i=1}^N\left (y_i\mathbb{log(}\hat{y_i}) (1- y_i)\mathbb{log}(1-\hat{y_i})\right) \\$

原理推导

由于只有分两类，因此同时也得到了正负类的概率，则可以假设样本服从伯努利分布（0-1分布） 。

$p(y_i=1|x_i) = \hat{y_i}\\ p(y_i=0|x_i) = 1-\hat{y_i} \\$

将两条式子合并成一条

$p(y_i|x_i) = (\hat{y_i})^{y_i} (1-\hat{y_i})^{1-y_i} \\$

假设数据点之间独立同分布，则似然函数，即各样本的概率乘机可以表示为

$L(x, y)=\prod_{i=1}^N(\hat{y_i})^{y_i} (1-\hat{y_i})^{1-y_i} \\$

对似然取对数，然后加负号变成最小化负对数似然，即为交叉熵损失函数的形式

$NLL(x, y)=J_{CE}=-\sum_{i=1}^N\left (y_i\mathbb{log(}\hat{y_i}) (1- y_i)\mathbb{log}(1-\hat{y_i})\right) \\$

3.1.2 多分类

在多分类的任务中，交叉熵损失函数的推导思路和二分类是一样的，变化的地方有两个：

真实值 $y_i$ 现在是一个 One-hot 向量，每个值代表每个类对应的概率，和为1
模型输出的激活函数由原来的 Sigmoid 函数换成 Softmax函数

Softmax 函数将每个维度的输出范围都限定在 $(0, 1)$ 之间，同时所有维度的输出和为 1，用于表示一个概率分布。

举例：假设一个5分类问题，然后一个样本I的标签y=[0,0,0,1,0]，也就是说样本I的真实标签是4。

假设模型预测的结果概率（softmax的输出）p=[0.1,0.15,0.05,0.6,0.1]，可以看出这个预测是对的，那么对应的损失L=-log(0.6)，也就是当这个样本经过这样的网络参数产生这样的预测p时，它的损失是-log(0.6)。

那么假设p=[0.15,0.2,0.4,0.1,0.15]，这个预测结果就很离谱了，因为真实标签是4，而你觉得这个样本是4的概率只有0.1（远不如其他概率高，如果是在测试阶段，那么模型就会预测该样本属于类别3），对应损失L=-log(0.1)。

再假设p=[0.05,0.15,0.4,0.3,0.1]，这个预测结果虽然也错了，但是没有前面那个那么离谱，对应的损失L=-log(0.3)。我们知道log函数在输入小于1的时候是个负数，而且log函数是递增函数，所以-log(0.6) < -log(0.3) < -log(0.1)。简单讲就是你预测错比预测对的损失要大，预测错得离谱比预测错得轻微的损失要大。

原理推导

我们知道Softmax 函数将每个维度的输出范围都限定在 $(0, 1)$ 之间，同时所有维度的输出和为 1，用于表示一个概率分布。那末对应类的概率可以表示为。

$p(y_i|x_i) = \prod_{k=1}^K(\hat{y_i}^k)^{y_i^k} \\$

假设模型输出 $\hat{y_i}$ =[0.1,0.15,0.05,0.6,0.1] ,真实样本为[0,0,0,1,0]，计算得p刚好为0.6,非1项的幂都为1了。

其中 $k \in K$ 表示 K 个类别中的一类，同样的假设数据点之间独立同分布，可得到负对数似然为

$NLL(x, y) = J_{CE} = -\sum_{i=1}^N\sum_{k=1}^K y_i^k \mathbb{log}(\hat{y_i}^k) \\$

由于 $y_i$ 是一个 one-hot 向量，除了目标类为 1 之外其他类别上的输出都为 0，因此上式也可以写为

$J_{CE} = -\sum_{i=1}^N y_i^{c_i}\mathbb{log}(\hat{y_i}^{c_i}) \\$

其中 $c_i$ 是样本 $x_i$ 的目标类。通常这个应用于多分类的交叉熵损失函数也被称为 Softmax Loss 或者 Categorical Cross Entropy Loss。

分类为什么是交叉熵

分类中为什么不用均方差损失？上文在介绍均方差损失的时候讲到实际上均方差损失假设了误差服从高斯分布，在分类任务下这个假设没办法被满足，因此效果会很差。为什么是交叉熵损失呢？有两个角度可以解释这个事情。

一个角度从最大似然的角度，也就是我们上面的推导，另一个角度是可以用信息论来解释交叉熵损失

以下是信息论的角度来解释。

假设对于样本 $x_i$ 存在一个最优分布 $y_i^{\star}$ 真实地表明了这个样本属于各个类别的概率，那么我们希望模型的输出 $\hat{y_i}$ 尽可能地逼近这个最优分布，在信息论中，我们可以使用 KL 散度来衡量两个分布的相似性。给定分布 $p$ 和分布 $q$ ，两者的 KL 散度公式如下

$KL(p, q)=\sum_{k=1}^Kp^k\mathbb{log}(p^k) - \sum_{k=1}^Kp^k\mathbb{log}(q^k) \\$

其中第一项为分布 $p$ 的信息熵，第二项为分布 $p$ 和 $q$ 的交叉熵。将最优分布 $y_i^{\star}$ 和输出分布 $\hat{y_i}$ 带入 $p$ 和 $q$ 得到

$KL(y_i^{\star}, \hat{y_i})=\sum_{k=1}^Ky_i^{\star k}\mathbb{log}(y_i^{\star k}) - \sum_{k=1}^Ky_i^{\star k}\mathbb{log}(\hat{y_i}^k) \\$

由于我们希望两个分布尽量相近，因此我们最小化 KL 散度。同时由于上式第一项信息熵仅与最优分布本身相关，因此我们在最小化的过程中可以忽略掉，变成最小化

$-\sum_{k=1}^Ky_i^{\star k}\mathbb{log}(\hat{y_i}^k) \\$

我们并不知道最优分布 $y_i^{\star}$ ，但训练数据里面的目标值 $y_i$ 可以看做是 $y_i^{\star}$ 的一个近似分布

$- \sum_{k=1}^Ky_i^k\mathbb{log}(\hat{y_i}^k) \\$

这个是针对单个训练样本的损失函数，如果考虑整个数据集，则

$J_{KL} = -\sum_{i=1}^N\sum_{k=1}^K y_i^k \mathbb{log}(\hat{y_i}^k)=-\sum_{i=1}^N y_i^{c_i}\mathbb{log}(\hat{y_i}^{c_i}) \\$

可以看到通过最小化交叉熵的角度推导出来的结果和使用最大化似然得到的结果是一致的。

总结

交叉熵函数与最大似然函数的联系和区别

区别：交叉熵函数使用来描述模型预测值和真实值的差距大小，越大代表越不相近；似然函数的本质就是衡量在某个参数下，整体的估计和真实的情况一样的概率，越大代表越相近。

联系：交叉熵函数可以由最大似然函数在伯努利分布的条件下推导出来，或者说最小化交叉熵函数的本质就是对数似然函数的最大化。

分类中的交叉熵损失相当于在数据分布为伯努利分布的情况下的log损失，均方损失相当于数据在高斯分布下的log损失，绝对值损失则是在拉普拉斯分布下的log损失。
通常在损失函数中还会有正则项（L1/L2 正则），这些正则项作为损失函数的一部分，通过约束参数的绝对值大小以及增加参数稀疏性来降低模型的复杂度，防止模型过拟合。